Что такое факторинг дебиторской задолженности
Совкомбанк Факторинг Контакты:Адрес: ул. Кожевническая, д. 14 115114 Москва, Телефон:(495) 787-53-37, Телефон:(495) 995-21-31, Электронная почта: [email protected]
Адрес2: ул. Рокоссовского, д. 62, БЦ «ВолгоградСИТИ», оф. 15-21 400050 г. Волгоград, Телефон:(8442) 43-44-00, Электронная почта: [email protected]
Адрес3:
ул.Свободы, д. 73, офис 311
394018
Россия, г. Воронеж,
Телефон:(473) 228-19-78, 228-19-79,
Электронная почта: sav_av@factoring.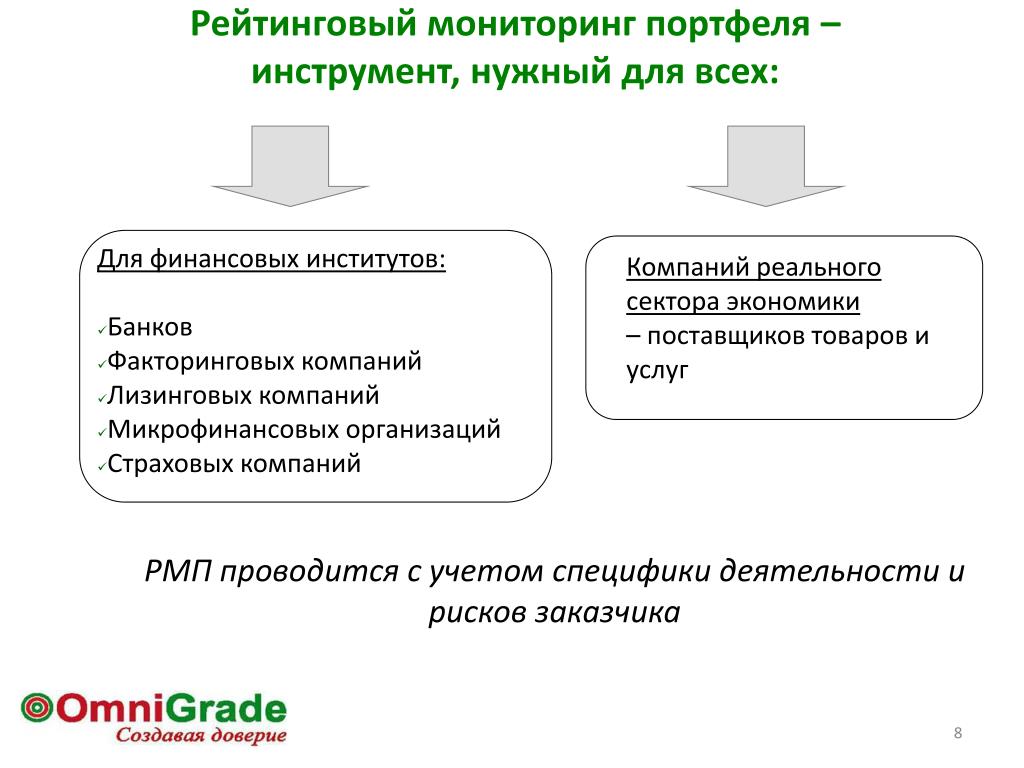
Адрес4: ул. Хохрякова, 10, оф. 504-505 620014 Свердловская область, г. Екатеринбург, Телефон:(343) 310-14-55, Электронная почта: [email protected]
Адрес5: ул. Рабочая, д. 2а, офис 29А (3952) 486 331 г. Иркутск, Телефон:(3952) 486 331, Электронная почта: [email protected]
Адрес6: ул. Декабристов, 85б, офис 409, 410 420034 г. Казань, Телефон:(843) 200-09-47, 200-10-35, Электронная почта: [email protected]
Адрес7:
Ленинский пр.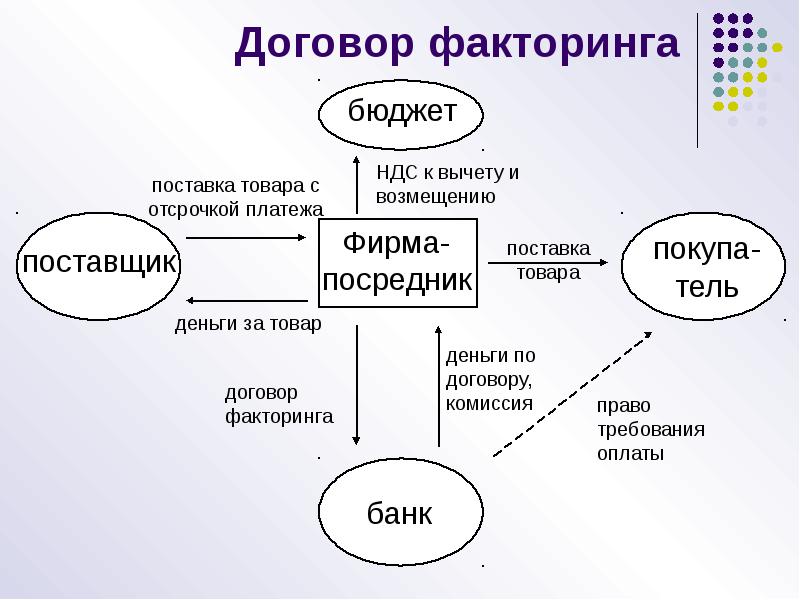 , д. 30, офис 508
236006
г. Калининград,
Телефон:(4012) 53-53-87,
Электронная почта: [email protected]
, д. 30, офис 508
236006
г. Калининград,
Телефон:(4012) 53-53-87,
Электронная почта: [email protected]
Адрес8: ул. Красная д. 152 г. Краснодар, Телефон:(861) 226-42-52, 226-45-54, Электронная почта: [email protected]
Адрес9: ул. Алексеева, д. 49, офис 6-14. 660077 г. Красноярск, Телефон:(391) 200-28-20, Электронная почта: [email protected]
Адрес10:
ул. Нижегородская, 24
603000
г.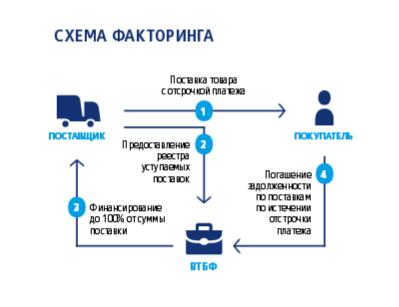 Нижний Новгород,
Телефон:(831) 288-02-89,
Электронная почта: [email protected]
Нижний Новгород,
Телефон:(831) 288-02-89,
Электронная почта: [email protected]
Адрес11: ул. Ленина, 52, офис 505 630004 г. Новосибирск, Телефон:(383) 212-06-18, 212-06-19, Электронная почта: [email protected]
Адрес12: ул. Николая Островского, 59/1 614007 г. Пермь, Телефон:(342) 211-50-28, Электронная почта: [email protected]
Адрес13:
ул. Красноармейская, д. 200, 8 этаж, оф. 803
344000
г. Ростов-на-Дону,
Телефон:(863) 263-88-30,
Электронная почта: kac_ay@factoring.
Адрес14: пр.К.Маркса, д.201 «Б» (бизнес-крепость «Башня») 443080 г. Самара, Телефон:(846)993-61-62, 993-61- 64, 993-61-63, Электронная почта: [email protected]
Адрес15: ул. Восстания, 18, офисы 405-407 191014 Санкт-Петербург, Телефон:(812) 644-40-71, Электронная почта: [email protected]
Адрес16: ул.Танкистов, д.37, оф.304, 305 410019 г. Саратов, Телефон:(8452) 57-27-63, Электронная почта: [email protected]
Адрес17:
ул. Крупской, д. 9, офис 727, 728, 729
450000
Республика Башкортостан, г. Уфа,
Телефон:(347) 273-50-78,
Электронная почта: [email protected]
Крупской, д. 9, офис 727, 728, 729
450000
Республика Башкортостан, г. Уфа,
Телефон:(347) 273-50-78,
Электронная почта: [email protected]
Адрес18: ул. К. Маркса, д.38, офис 319 454091 г. Челябинск, Телефон:(351) 239-93-90, 239-93-91, 239-93-92, Электронная почта: [email protected]
Адрес19: ул. Республиканская, д.3, корпус 1, офис 404 150003 г. Ярославль, Телефон:(4852) 58-11-88, Электронная почта: [email protected]
Что такое факторинг дебиторской задолженности
Совкомбанк Факторинг Контакты: Адрес:
ул. Кожевническая, д. 14
115114
Москва,
Телефон:(495) 787-53-37,
Телефон:(495) 995-21-31,
Электронная почта: [email protected]
Кожевническая, д. 14
115114
Москва,
Телефон:(495) 787-53-37,
Телефон:(495) 995-21-31,
Электронная почта: [email protected]
Адрес2: ул. Рокоссовского, д. 62, БЦ «ВолгоградСИТИ», оф. 15-21 400050 г. Волгоград, Телефон:(8442) 43-44-00, Электронная почта: [email protected]
Адрес3: ул.Свободы, д. 73, офис 311 394018 Россия, г. Воронеж, Телефон:(473) 228-19-78, 228-19-79, Электронная почта: [email protected]
Адрес4:
ул.
Адрес5: ул. Рабочая, д. 2а, офис 29А (3952) 486 331 г. Иркутск, Телефон:(3952) 486 331, Электронная почта: [email protected]
Адрес6: ул. Декабристов, 85б, офис 409, 410 420034 г. Казань, Телефон:(843) 200-09-47, 200-10-35, Электронная почта: [email protected]
Адрес7:
Ленинский пр.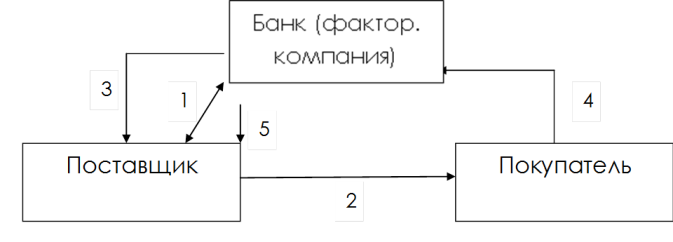 , д. 30, офис 508
236006
г. Калининград,
Телефон:(4012) 53-53-87,
Электронная почта: [email protected]
, д. 30, офис 508
236006
г. Калининград,
Телефон:(4012) 53-53-87,
Электронная почта: [email protected]
Адрес8: ул. Красная д. 152 г. Краснодар, Телефон:(861) 226-42-52, 226-45-54, Электронная почта: [email protected]
Адрес9: ул. Алексеева, д. 49, офис 6-14. 660077 г. Красноярск, Телефон:(391) 200-28-20, Электронная почта: [email protected]
Адрес10:
ул. Нижегородская, 24
603000
г.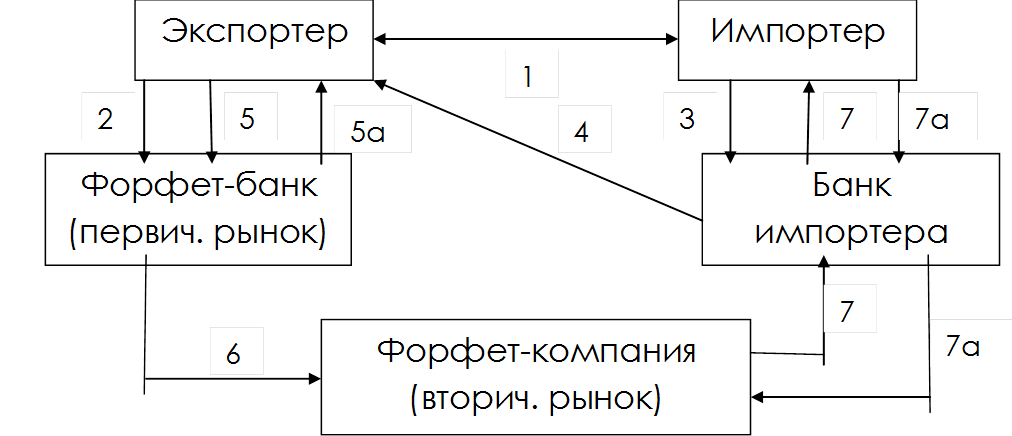 Нижний Новгород,
Телефон:(831) 288-02-89,
Электронная почта: [email protected]
Нижний Новгород,
Телефон:(831) 288-02-89,
Электронная почта: [email protected]
Адрес11: ул. Ленина, 52, офис 505 630004 г. Новосибирск, Телефон:(383) 212-06-18, 212-06-19, Электронная почта: [email protected]
Адрес12: ул. Николая Островского, 59/1 614007 г. Пермь, Телефон:(342) 211-50-28, Электронная почта: [email protected]
Адрес13:
ул. Красноармейская, д. 200, 8 этаж, оф. 803
344000
г. Ростов-на-Дону,
Телефон:(863) 263-88-30,
Электронная почта: kac_ay@factoring. ru
ru
Адрес14: пр.К.Маркса, д.201 «Б» (бизнес-крепость «Башня») 443080 г. Самара, Телефон:(846)993-61-62, 993-61- 64, 993-61-63, Электронная почта: [email protected]
Адрес15: ул. Восстания, 18, офисы 405-407 191014 Санкт-Петербург, Телефон:(812) 644-40-71, Электронная почта: [email protected]
Адрес16: ул.Танкистов, д.37, оф.304, 305 410019 г. Саратов, Телефон:(8452) 57-27-63, Электронная почта: [email protected]
Адрес17:
ул. Крупской, д. 9, офис 727, 728, 729
450000
Республика Башкортостан, г. Уфа,
Телефон:(347) 273-50-78,
Электронная почта: [email protected]
Крупской, д. 9, офис 727, 728, 729
450000
Республика Башкортостан, г. Уфа,
Телефон:(347) 273-50-78,
Электронная почта: [email protected]
Адрес18: ул. К. Маркса, д.38, офис 319 454091 г. Челябинск, Телефон:(351) 239-93-90, 239-93-91, 239-93-92, Электронная почта: [email protected]
Адрес19: ул. Республиканская, д.3, корпус 1, офис 404 150003 г. Ярославль, Телефон:(4852) 58-11-88, Электронная почта: [email protected]
Международный факторинг
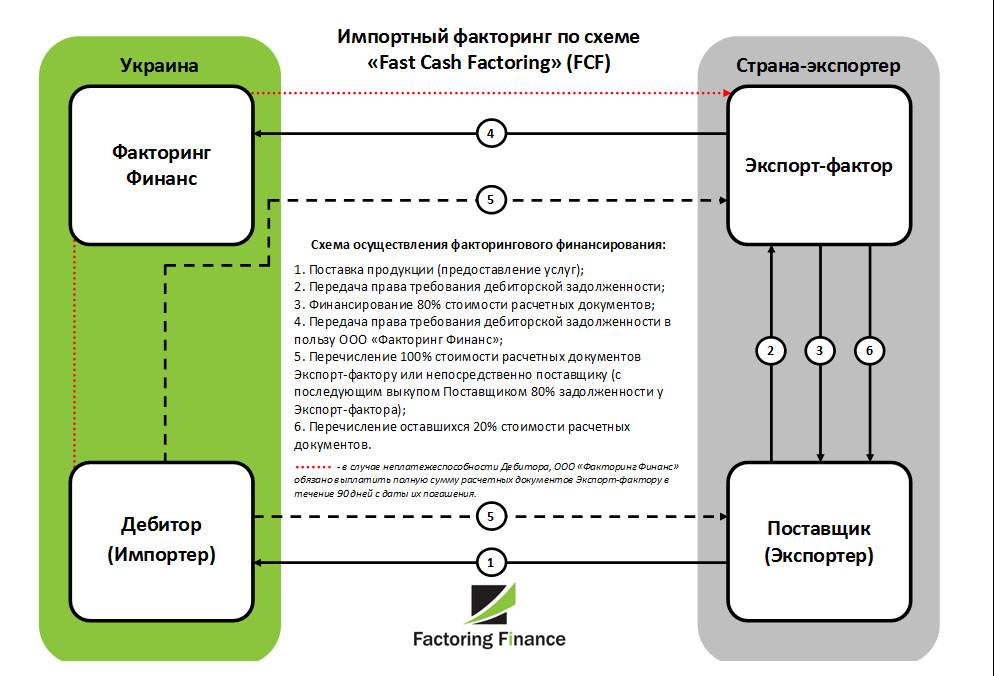
Международный факторинг – вид факторинговой операции, обеспечивающий расчеты и сервисное сопровождение финансирования поставок товаров и услуг с отсрочкой платежа в условиях, когда поставщик и покупатель являются резидентами разных государств. Международный факторинг, в отличие от операций по торговому финансированию, используется для работы по долгосрочным или бессрочным внешнеэкономическим контрактам, характеризующимся регулярностью поставок и тенденцией к увеличению товарооборота. Международный факторинг осуществляется по двум моделям: однофакторной и двухфакторной.
Международный факторинг, в отличие от операций по торговому финансированию, используется для работы по долгосрочным или бессрочным внешнеэкономическим контрактам, характеризующимся регулярностью поставок и тенденцией к увеличению товарооборота. Международный факторинг осуществляется по двум моделям: однофакторной и двухфакторной.
Однофакторная модель предусматривает оказание комплекса услуг международного факторинга, при котором Фактор и компания-клиент являются резидентами одного государства. Однофакторная модель преимущественно используется при экспортных операциях.
Двухфакторная модель предусматривает разделение функций международного факторинга между двумя факторами, являющимися резидентами двух стран, которые представляют поставщик и покупатель соответственно. В результате расчеты и факторинговый сервис предоставляются как поставщику-резиденту, так и покупателю-нерезиденту.
Экспорт-фактор — банк или специализированная факторинговая компания, предоставляющие услуги международного факторинга поставщику-экспортеру. В функции Экспорт-фактора могут входить осуществление трансграничных расчетов по внешнеторговым контрактам, финансирование поставщика-экспортера в объеме выручки по экспортному контракту (полностью либо частично), покрытие риска неплатежа со стороны покупателя-нерезидента, а также получение выручки с покупателя-нерезидента.
В функции Экспорт-фактора могут входить осуществление трансграничных расчетов по внешнеторговым контрактам, финансирование поставщика-экспортера в объеме выручки по экспортному контракту (полностью либо частично), покрытие риска неплатежа со стороны покупателя-нерезидента, а также получение выручки с покупателя-нерезидента.
Импорт-фактор — банк или специализированная факторинговая компания, предоставляющая услуги международного факторинга в стране покупателя-нерезидента. Импорт-фактор задействуется при реализации двухфакторной модели международного факторинга. В функции Импорт-фактора могут входить осуществление трансграничных расчетов по внешнеторговым контрактам, покрытие риска неплатежа со стороны покупателя-нерезидента, получение выручки с покупателя-нерезидента.
Договор международного факторинга – двусторонний договор о факторинговом обслуживании, заключаемый между резидентами одного государства. Условия договора зависят от вида торговой операции (экспорт или импорт), осуществляемой компанией-резидентом.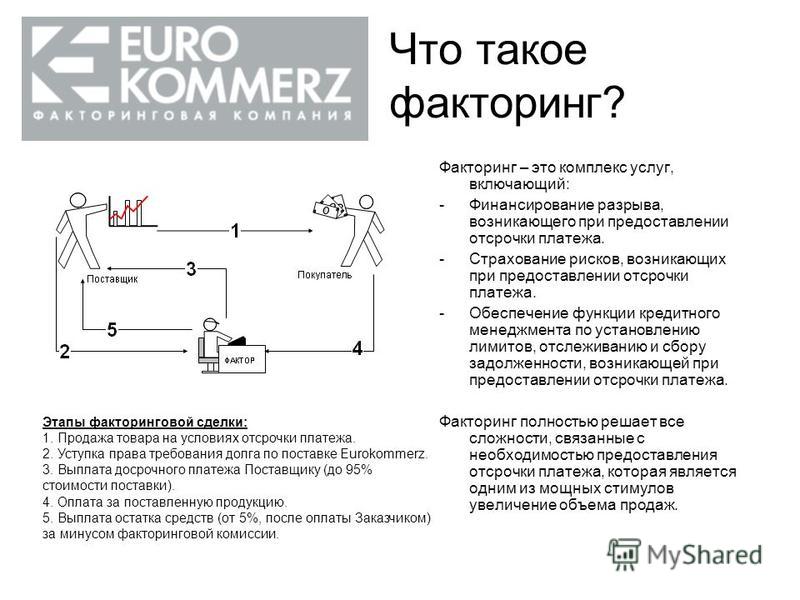
Внешнеторговый контракт – договор на поставку товаров либо оказание услуг, заключаемый между российской и зарубежной компанией. Копия контракта предоставляется при заключении договора международного факторинга наряду с документами, подтверждающими факт поставки (invoice). Для целей международного факторинга во внешнеторговом контракте должен быть предусмотрен порядок расчетов на условиях отсрочки платежа.
Международная факторинговая ассоциация – организация, под эгидой которой осуществляется взаимодействие Экспорт-фактора и Импорт-фактора при реализации международного факторинга по двухфакторной модели. Банк или специализированная компания в России должны являться членами одной из двух МФА – Factors Chain International и/или International Factors Group.
Виды международного факторинга
Документы, регулирующие международный факторинг
Что такое факторинг | Схема, виды, этапы
Факторинг — это система финансовых услуг для производителей и поставщиков, которые продают свои товары и услуги на условиях отсрочки платежей.
Бывает, что организациям приходится выбирать: работать по предоплате или дать отсрочку. Если выбрать первый вариант, то некоторые клиенты откажутся от сотрудничества из-за невыгодных условий. Второй вариант может привести к тому, что у компании не останется денег для текущих расходов, и она обанкротится.
Факторинг поможет принять решение. Простыми словами — это своеобразная форма кредита для покупателя на оплату поставки товаров и услуг. Производитель или поставщик услуг передаёт право на задолженность посреднику — фактору. Это помогает получить оплату быстрее.
Выступать в роли фактора может факторинговая компания или банк.
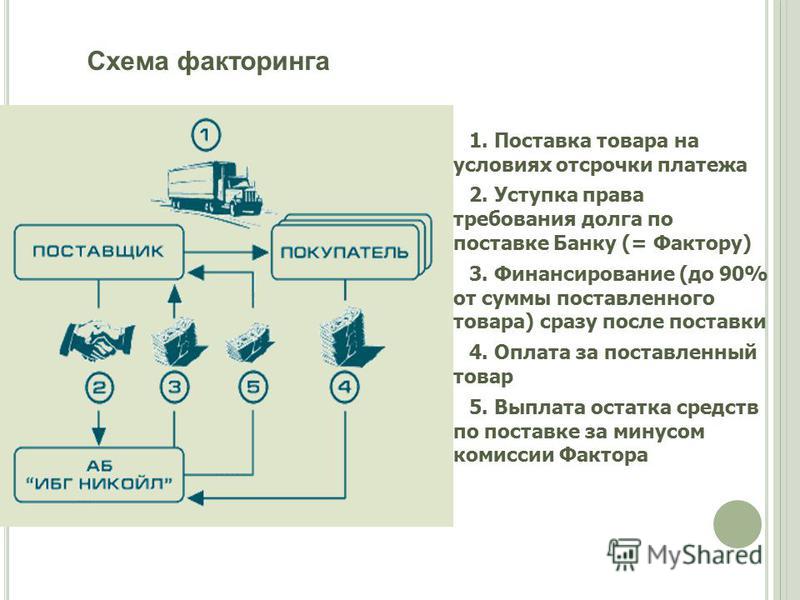
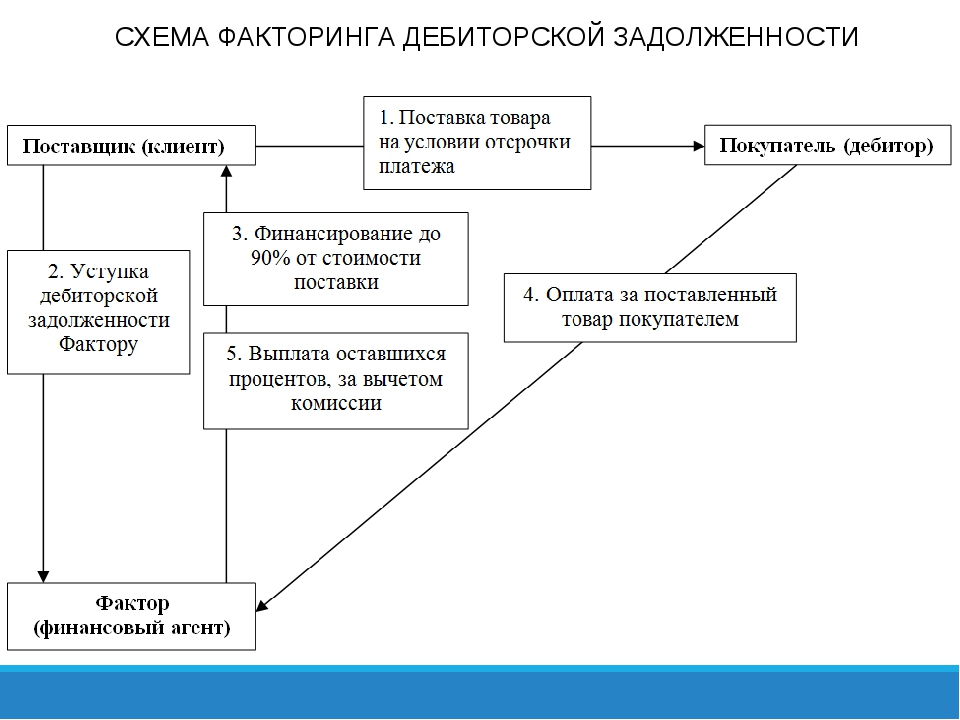
Схема факторинга
В факторинге всегда участвуют три стороны:
-
Поставщик товара — клиент факторинговой компании или отдела банка, кредитор.
-
Покупатель — дебитор.
-
Фактор — факторинговая компания или отдел банка.

Самая распространённая схема реализации факторинга состоит из четырёх шагов.
Шаг 1. Поставщик договаривается с покупателем об отсрочке платежа и отгружает товар. Отсрочка может составлять от одной недели до четырёх месяцев.
Шаг 2. Поставщик подписывает договор с фактором и передаёт ему накладные.
Шаг 3. Фактор выплачивает 90% от общей стоимости поставки по накладным. Оставшуюся сумму выплачивают после того, как покупатель получит и проверит товар.
Шаг 4. Покупатель выплачивает задолженность фактору.
Виды факторинга
Существует несколько классификаций факторинга. Вот основные из них.
По способу информирования:
- Открытый факторинг — поставщик сообщил покупателю о заключении договора с фактором, и покупатель выплачивает задолженность фактору.
- Закрытый факторинг — поставщик не сообщает покупателю о факторинговой сделке.
 Покупатель выплачивает деньги поставщику, который расплачивается с фактором.
Покупатель выплачивает деньги поставщику, который расплачивается с фактором.
По распределению рисков факторинг может быть:
- С правом регресса — если должник нарушил договор, то фактор возвращает неоплаченные счета и требует вернуть деньги.
- Без права регресса — все риски берёт на себя факторинговая компания, и в случае взыскания долга покрывает все судебные издержки.
По времени возникновения долга факторинг может быть реальным, если договор заключают, когда уже наступили долговые обязательства, и консенсуальным, если долг переуступается заранее.
По резидентности участников факторинг бывает внутренним, если все участники — резиденты одной страны, и внешним, то есть международным.
В сделке может участвовать один или два фактора. В зависимости от этого факторинг бывает прямым и взаимным.
По спектру услуг:
- Широкий или конвенционный факторинг, если факторинговая компания, кроме финансирования и инкассации долга, предоставляет бухгалтерские, страховые и другие услуги;
- Узкий или ограниченный подразумевает, что перечень услуг ограничен основными функциями факторинга.

По виду документооборота факторинг бывает традиционным и электронным, если все документы оформляются и передаются в электронном виде.
Этапы факторинга
1. Перед заключением договора оцениваются финансовые возможности клиента. Поставщик предоставляет фактору информацию о покупателе, условиях доставки, оплаты, случаях нарушения договоров.
2. Подготовка и заключение договора факторинга. В договоре указывают:
- предмет договора
- права и обязанности сторон
- процедуру финансирования
- кредитный лимит
- условия передачи фактору права на долг
- стоимость услуг фактора и порядок расчёта
- действия при нарушении обязательств дебитором
- срок договора и другие условия.
3. Контроль сделки. В период действия договора важно, чтобы все участники исполняли обязательства. Если договор нарушен, оформляют претензию.
Факторинговая компания тоже может провести переоценку поставщика и покупателя и проконтролировать, что задействованные активы соответствуют требованиям по договору.
🎁
Новым ИП — год Эльбы в подарок
Год онлайн-бухгалтерии на тарифе Премиум для ИП младше 3 месяцев
Попробовать бесплатноКогда факторинг полезен для предпринимателя
С помощью факторинга компании могут в короткие сроки увеличить оборотный капитал. Факторинг оказывается дешевле краткосрочных кредитов.
Компании прибегают к этой системе финансирования, когда хотят привлечь покупателей, предлагая удобные способы оплаты.
Кто не может пользоваться факторингом
Компании, которые
- выпускают специализированные товары,
- выставляют счета после выполнения определённых работ,
- имеют много покупателей, которые не оплатили товары и услуги,
- работают с субподрядчиками,
- работают на условиях постпродажного обслуживания.

Факторинг не используют для расчётов между филиалами одной организации и погашения долговых обязательств физлиц и бюджетных организаций.
Статья актуальна на
Факторинг: понятие, функции и преимущества
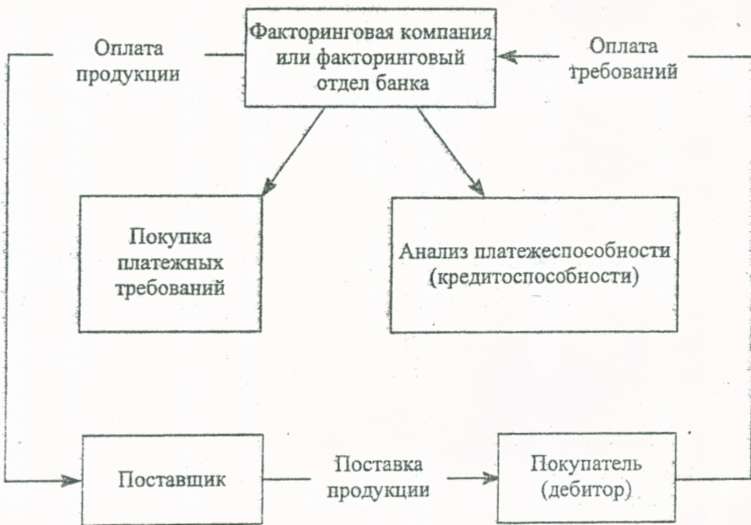
В настоящее время многие поставщики испытывают затруднения с получением средств от дебиторов, поскольку последние задерживают платежи. Отсутствие оборотных средств у поставщиков затрудняет следующие поставки и делает невозможным дальнейшее развитие бизнеса. Одним из способов справиться с этой ситуацией являются услуги факторинговых компаний.
Деятельность факторинговой компании заключается в кредитовании поставщика посредством выкупа дебиторской задолженности. То есть факторинговая компания выдает поставщику 90 % стоимости его поставки и берет на себя все заботы, связанные с взысканием платежа с клиента.
Таким образом, компании малого и среднего бизнеса получают средства для роста и развития своего производства, а факторинговая компания берет процент за свои услуги (около 1 % от суммы поставки).
Елена Гладких, генеральный директор и основатель русской факторинговой компании, отмечает, что в последнее время появилась возможность предоставить клиентам 100 % финансирования. Если платежная дисциплина клиента и надежность дебиторов не вызывает сомнений, факторинговая фирма может пойти на риск и предоставить 100 % суммы поставки, а позже получить свой процент за услуги.
Кроме того, Елена Гладких сообщила, что русская факторинговая компания предоставляет комплексные услуги, начиная от финансирования закупки сырья и заканчивая выкупом дебиторской задолженности. Генеральный директор заметила, что комплексный подход достаточно востребован за счет удобства и возможностей для роста компании-поставщика.
Также Елена Гладких отметила еще одно преимущество факторинговых компаний – индивидуальный подход к каждому клиенту. В отличие от банков, основным критерием для выдачи кредита в факторинговой компании является надежность и качество дебиторов. Если клиент может объяснить, почему у его компании убыточный баланс, и при этом спрос на его продукцию достаточно велик, русская факторинговая компания может начать сотрудничество и предоставить кредит.
Дальневосточный вебинар «Факторинг: привлечение финансирования для малого и среднего бизнеса»
Банк России приглашает принять участие в дальневосточном вебинаре «Факторинг: привлечение финансирования для малого и среднего бизнеса»
Дата: 18 февраля 2021 г.
Начало: 09.30 (мск)
На вебинаре вы узнаете:
- Что такое факторинг, зачем он нужен, виды факторинга;
- Почему факторинг удобен для привлечения оборотного капитала;
- Почему факторинг – альтернатива банковскому кредитованию;
- Факторинг на Дальнем Востоке: региональная практика факторинговых сделок;
- О цифровизации факторинговых услуг.
Продолжительность вебинара – 2 часа.
Спикеры: эксперты Банка России, представители Ассоциации факторинговых компаний, факторов и организаций, имеющих опыт факторинговых сделок.
Чтобы получить доступ к трансляции и иметь возможность задать вопрос спикерам, необходимо зарегистрироваться на мероприятие по ссылке. https://forms.yandex.ru/u/601c844695d825393019a819/
https://forms.yandex.ru/u/601c844695d825393019a819/
С программой можно ознакомиться здесь.
Дальневосточный вебинар
«Факторинг: привлечение финансирования
для малого и среднего бизнеса»
18 февраля 2021 г. (четверг)
09.30-11.30 (мск)
Модератор: Божор Юрий Анатольевич, руководитель экспертной группы Управления финансовой доступности Банка России
Продолжительность: 09.30-11.30 (время московское)
09.30-09.35 | Приветственное слово Давыдов Денис Витальевич, заместитель начальника Дальневосточного ГУ Банка России (г. Владивосток) |
09.35-09.50
| Факторинг как удобный способ привлечения оборотного капитала, альтернативный банковскому кредитованию Божор Юрий Анатольевич, руководитель экспертной группы Управления финансовой доступности Банка России (г. |
09.50-10.05
| Понятие, виды и функции факторинга Вернов Виктор Алексеевич, генеральный директор ООО «Факторинг ПЛЮС», член Правления Ассоциации факторинговых компаний (АФК), (г. Москва) |
10.05-10.35
| Текущая и потенциальная востребованность факторинга на Дальнем Востоке. Региональная практика факторинговых сделок |
10.05-10.15 | Носов Роман Геннадьевич, директор по развитию бизнеса Региона «Дальний Восток», ООО ВТБ Факторинг (г. Хабаровск) |
10.15-10.25 | Евдокимова Светлана Михайловна, генеральный директор компании «Инвест-Бизнес Лизинг» (г. Якутск) |
10.25-10. | Мамедов Алиш Забид Оглы, генеральный директор АО «Якутцемент» (г. Якутск) |
10.35-10.50
| О цифровизации факторинговых услуг Газетин Егор Александрович, генеральный директор GetFinance (г. Москва) |
10.50-11.30 | Открытый микрофон |
Факторинг — инструмент оценки, анализа и развития отношений с покупателями
Крупные компании могут диктовать свои условия торговым партнерам, а малый и средний бизнес, напротив, лишен такой возможности. Это вынуждает компании рисковать при принятии решения о сотрудничестве с новыми партнерами в отсутствие необходимого анализа и информации для принятия правильного решения, давать свой товар в кредит или нет.
Факторинговая компания может брать на себя следующие функции:
• проверка покупателей заемщика до заключения договора;
• кредитный контроль в ходе реализации кредитного договора: выявление просрочек, установление их причин, переговоры с покупателями;
• контроль установленных условий сотрудничества с покупателями в рамках договора поставки.
Факторинг дает компаниям возможность значительно расширить круг своих покупателей. Во-первых, этот инструмент позволяет финансировать поставки с отсрочкой платежа. Многие покупатели готовы увеличивать объемы закупок только на условиях отсрочки. Поэтому благодаря факторингу клиент может существенно расширить объем сбыта, предложив потенциальным покупателям схему: отсрочка платежа + факторинг. Однако возникает вопрос оценки надежности и платежеспособности контрагентов. Эту функцию на себя берет факторинговая компания.
Проверка покупателей может проводиться перед заключением договора поставки с отсрочкой платежа и быть условием для его действия. По результатам проверки клиент получает оценку своего контрагента, а также рекомендации по размеру кредитного лимита и возможности работы с отсрочкой платежа. Такая мера особенно актуальна для небольших компаний, у которых нет штата специалистов для проведения соответствующих проверок.
По результатам проверки клиент получает оценку своего контрагента, а также рекомендации по размеру кредитного лимита и возможности работы с отсрочкой платежа. Такая мера особенно актуальна для небольших компаний, у которых нет штата специалистов для проведения соответствующих проверок.
Подобная оценка может быть полезна и для банков, которые кредитуют своих клиентов. Неспособность заемщика профессионально управлять своей дебиторской задолженностью (которая является его основным активом) и коммерческим кредитованием своих покупателей с высокой вероятностью создает риски для банка или факторинговой компании. В свою очередь, банк также не обладает необходимыми навыками для контроля и создания системы кредитного менеджмента (управления кредитованием покупателей) на предприятиях. В этом плане у факторинговых компаний явное преимущество, поскольку они как раз обычно имеют специалистов соответствующей квалификации.
В этом случае факторинговая компания проводит оценку портфеля дебиторской задолженности заемщика и анализирует его кредитную политику. Банк определяет необходимый уровень детализации параметров для проверки и может учитывать или не учитывать ее результаты при принятии решения о кредитовании. Он может также использовать рекомендации, полученные при проверке, в качестве обязательных для заемщика условий получения кредита.
Банк определяет необходимый уровень детализации параметров для проверки и может учитывать или не учитывать ее результаты при принятии решения о кредитовании. Он может также использовать рекомендации, полученные при проверке, в качестве обязательных для заемщика условий получения кредита.
Передача дебиторской задолженности в управление специализированной организации, уполномоченной банком, может стать условием действия кредитного договора. Это позволит банку снизить уровень кредитного риска по сделке, а заемщику — повысить эффективность работы с покупателями.
При такой схеме работы банк заранее согласует набор действий, которые предпринимаются при просрочке платежа покупателем заемщика. Заемщик заключает договор об управлении дебиторской задолженностью с уполномоченной компанией банка и только после этого может получить финансирование в рамках кредита.
В роли подобных специализированных компаний успешно выступают факторинговые компании, обладающие всеми необходимыми компетенциями для этого.
Реклама
Факторинговая квадратичность
«Факторинг» (или «Факторинг» в Великобритании) Квадратичный равен:
найти, что умножить, чтобы получить квадратичный
Это называется «факторинг», потому что мы находим коэффициенты (коэффициент — это то, на что мы умножаем)
Пример:
Умножение (x + 4) и (x − 1) вместе (так называемое расширение) дает x 2 + 3x — 4 :
Таким образом, (x + 4) и (x − 1) являются множителями x 2 + 3x — 4
На всякий случай проверим:
(х + 4) (x − 1) = x (x − 1) + 4 (x − 1)
= х 2 — х + 4х — 4
= х 2 + 3х — 4Да, (x + 4) и (x − 1) определенно являются множителями x 2 + 3x — 4
Вы видели, что расширение и факторинг — противоположности?
Расширение обычно легко, но факторинг часто бывает сложным .
Это все равно, что пытаться найти, какие ингредиенты
пошли на торт, чтобы сделать его таким вкусным.
Это сложно понять!
Итак, давайте попробуем пример, где мы еще не знаем факторов:
Общий коэффициент
Сначала проверьте, есть ли общие факторы.
Пример: каковы множители 6x
2 — 2x = 0?6 и 2 имеют общий множитель 2 :
2 (3x 2 — x) = 0
И x 2 и x имеют общий множитель x :
2x (3x — 1) = 0
И мы это сделали! Коэффициенты: 2x и 3x — 1 ,
.Теперь мы также можем найти корни (где он равен нулю):
- 2x равно 0, когда x = 0
- 3x — 1 равно нулю, когда x = 1 3
А это график (посмотрите, как он равен нулю при x = 0 и x = 1 3 ):
Но это не всегда так просто.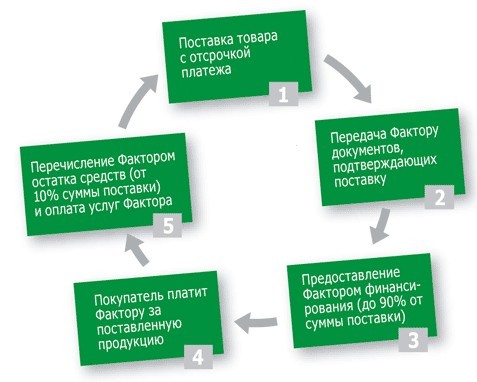 ..
..
Угадай и проверь
Может, ответ дадим?
Пример: каковы множители 2x
2 + 7x + 3?Нет общих факторов.
Давайте попробуем угадать ответ, а затем проверим, правы ли мы … нам может повезти!
Мы могли угадать (2x + 3) (x + 1):
(2x + 3) (x + 1) = 2x 2 + 2x + 3x + 3
= 2x 2 + 5x + 3 (НЕПРАВИЛЬНО)
Как насчет (2x + 7) (x − 1):
(2x + 7) (x − 1) = 2x 2 — 2x + 7x — 7
= 2x 2 + 5x — 7 (СНОВА НЕПРАВИЛЬНО)
Хорошо, как насчет (2x + 9) (x − 1):
(2x + 9) (x − 1) = 2x 2 — 2x + 9x — 9
= 2x 2 + 7x — 9 (СНОВА НЕПРАВИЛЬНО)
О нет! Мы можем долго гадать, прежде чем нам повезет.
Это не очень хороший метод. Так что давайте попробуем что-нибудь еще.
Так что давайте попробуем что-нибудь еще.
Метод для простых случаев
К счастью, есть метод, который работает в простых случаях.
С квадратным уравнением в этой форме:
Шаг 1 : Найдите два числа, которые умножаются, чтобы получить ac (другими словами, a на c), и сложить, чтобы получить b.
Пример: 2x 2 + 7x + 3
ac равно 2 × 3 = 6 , а b равно 7
Итак, мы хотим, чтобы два числа, которые умножались вместе, давали 6 и в сумме давали 7
Фактически это делают 6 и 1 (6 × 1 = 6 и 6 + 1 = 7)
Как найти 6 и 1?
Это помогает составить список факторов ac = 6 , а затем попытаться добавить некоторые, чтобы получить b = 7 .
Факторы 6 включают 1, 2, 3 и 6.
Ага! 1 и 6 прибавляются к 7, а 6 × 1 = 6.
Шаг 2 : Перепишите середину с этими числами:
Перепишите 7x с 6 x и 1 x:
2x 2 + 6x + x + 3
Шаг 3 : Разложите на множители первые два и последние два термина по отдельности:
Первые два члена 2x 2 + 6x разложить на 2x (x + 3)
Последние два члена x + 3 в данном случае фактически не меняются
Получаем:
2х (х + 3) + (х + 3)
Шаг 4 : Если мы сделали это правильно, два наших новых члена должны иметь четко видимый общий множитель.
В этом случае мы видим, что (x + 3) является общим для обоих терминов, поэтому мы можем пойти:
Начать с: 2x (x + 3) + (x + 3)
Что составляет: 2x (x + 3) + 1 (x + 3)
И так: (2x + 1) (x + 3)
Готово!
Проверить: (2x + 1) (x + 3) = 2x 2 + 6x + x + 3 = 2x 2 + 7x + 3 (Да)
Намного лучше, чем гадать!
Давайте снова посмотрим шаги с 1 по 4 за один раз :
| 2x 2 + 7x + 3 |
| 2x 2 + 6x + x + 3 |
| 2x (x + 3) + (x + 3) |
| 2x (x + 3) + 1 (x + 3) |
| (2x + 1) (x + 3) |
Хорошо, давайте попробуем другой пример:
Пример: 6x
2 + 5x — 6Шаг 1 : ac равно 6 × (−6) = −36 , а b равно 5
Перечислите положительные множители ac = −36 : 1, 2, 3, 4, 6, 9, 12, 18, 36
Одно из чисел должно быть отрицательным, чтобы получилось −36, поэтому, играя с несколькими разными числами, я обнаружил, что −4 и 9 работают хорошо:
−4 × 9 = −36 и −4 + 9 = 5
Шаг 2 : перепишите 5x с −4x и 9x:
6x 2 — 4x + 9x — 6
Шаг 3 : Разложите на множители первые два и последние два:
2x (3x — 2) + 3 (3x — 2)
Шаг 4 : Общий множитель (3x — 2):
(2x + 3) (3x — 2)
Проверить: (2x + 3) (3x — 2) = 6x 2 — 4x + 9x — 6 = 6x 2 + 5x — 6 (Да)
В поисках чисел
Самая сложная часть — найти два числа, которые умножаются, чтобы получить ac, и складывать, чтобы получить b.
Это отчасти предположение, и помогает перечислить все факторы .
Вот еще один пример, который может вам помочь:
Пример: ac = −120 и b = 7
Какие два числа умножают на -120, и добавляют к 7 ?
Множитель 120 (плюс и минус):
1, 2, 3, 4, 5, 6, 8, 10, 12, 15, 20, 24, 30, 40, 60 и 120
Мы можем попробовать пары множителей (начнем с середины!) И посмотреть, прибавят ли они к 7:
- −10 x 12 = −120 и −10 + 12 = 2 (нет)
- −8 x 15 = −120 и −8 + 15 = 7 (ДА!)
Попрактикуйтесь
Почему фактор?
Что ж, одно из больших преимуществ факторизации состоит в том, что мы можем найти корней квадратного уравнения (где уравнение равно нулю).
Все, что нам нужно сделать (после факторинга), это найти, где каждый из двух множителей становится равным нулю
Пример: каковы корни (нули) числа 6x
2 + 5x — 6?Мы уже знаем (сверху) коэффициенты
(2x + 3) (3x — 2)
И мы можем выяснить, что
(2x + 3) равно нулю, когда x = −3/2
и
(3x — 2) равно нулю, когда x = 2/3
Итак, корни 6x 2 + 5x — 6 равны:
−3/2 и 2/3
Вот график 6x 2 + 5x — 6, видите, где он равен нулю?
И мы также можем проверить это с помощью небольшой арифметики:
При x = -3/2: 6 (-3/2) 2 + 5 (-3/2) — 6 = 6 × (9/4) — 15/2 — 6 = 54/4 — 15 / 2-6 = 6-6 = 0
При x = 2/3: 6 (2/3) 2 + 5 (2/3) — 6 = 6 × (4/9) + 10/3 — 6 = 24/9 + 10/3 — 6 = 6-6 = 0
Графики
Мы также можем попробовать построить квадратное уравнение. Увидев, где он равен нулю, мы можем понять.
Увидев, где он равен нулю, мы можем понять.
Пример: (продолжение)
Начиная с 6x 2 + 5x — 6 и только этот участок:
Корни равны около x = −1,5 и x = +0,67, поэтому мы можем предположить , что корни равны:
−3/2 и 2/3
Что может помочь нам определить факторы 2x + 3 и 3x — 2
Всегда проверяйте! На графике значение +0.67 может и не быть 2/3
Общее решение
Существует также общее решение (полезно, когда описанный выше метод не работает), в котором используется формула корней квадратного уравнения:
Используйте эту формулу, чтобы получить два ответа x + и x — (один для случая «+», а другой для случая «-» в «±»), и мы получим это факторинг :
а (х — х + ) (х — х — )
Давайте воспользуемся предыдущим примером, чтобы увидеть, как это работает:
Пример: каковы корни у 6x
2 + 5x — 6?Подставляем a = 6, b = 5 и c = −6 в формулу:
x = −b ± √ (b 2 — 4ac) 2a
= −5 ± √ (5 2 — 4 × 6 × (−6)) 2 × 6
= −5 ± √ (25 + 144) 12
= −5 ± √169 12
= −5 ± 13 12
Итак, два корня:
х + = (-5 + 13) / 12 = 8/12 = 2/3,
x — = (−5 — 13) / 12 = −18/12 = −3/2
(Обратите внимание, что мы получаем тот же ответ, что и при факторинге ранее. )
)
Теперь поместите эти значения в (x — x + ) (x — x — ):
6 (х — 2/3) (х + 3/2)
Мы можем немного изменить это, чтобы упростить:
3 (х — 2/3) × 2 (х + 3/2) = (3x — 2) (2x + 3)
И мы получаем те же факторы, что и раньше.
362, 1203, 2262, 363, 1204, 2263, 2100, 2101, 2102, 2103, 2264, 2265
(Спасибо «mathsyperson» за части этой статьи)
Алгебра — разложение многочленов
Показать уведомление для мобильных устройств Показать все заметки Скрыть все заметки Похоже, вы используете устройство с «узкой» шириной экрана ( i. е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
е. вы, вероятно, пользуетесь мобильным телефоном). Из-за особенностей математики на этом сайте лучше всего просматривать в ландшафтном режиме. Если ваше устройство не находится в альбомном режиме, многие уравнения будут отображаться сбоку от вашего устройства (вы должны иметь возможность прокручивать, чтобы увидеть их), а некоторые элементы меню будут обрезаны из-за узкой ширины экрана.
Раздел 1-5: Факторинг многочленов
Из всех тем, затронутых в этой главе, разложение на множители многочленов, вероятно, является наиболее важной.В следующих главах есть много разделов, в которых первым шагом будет факторизация многочлена. Итак, если вы не можете разложить многочлен на множители, вы не сможете даже начать задачу, не говоря уже о ее завершении.
Давайте начнем с того, что немного поговорим о том, что такое факторинг. Факторинг — это процесс, с помощью которого мы определяем, на что мы умножили, чтобы получить заданное количество. Мы все время делаем это с числами. Например, вот несколько способов множителя 12.
Мы все время делаем это с числами. Например, вот несколько способов множителя 12.
Есть еще много возможных способов множителя 12, но они типичны для многих из них.
Обычный метод разложения чисел на множители состоит в том, чтобы полностью разложить числа на положительные простые множители. Простое число — это число, единственные положительные делители которого равны 1 и самому себе. Например, 2, 3, 5 и 7 являются примерами простых чисел. Примеры непростых чисел: 4, 6 и 12, чтобы выбрать несколько.
Примеры непростых чисел: 4, 6 и 12, чтобы выбрать несколько.
Если мы полностью разложим число на положительные простые множители, это будет только один способ сделать это. Это причина такого факторинга.Для нашего примера выше с 12 полная факторизация:
\ [12 = \ влево (2 \ вправо) \ влево (2 \ вправо) \ влево (3 \ вправо) \] Факторизация многочленов выполняется примерно таким же образом. Мы определяем все члены, которые были перемножены, чтобы получить заданный многочлен. Затем мы пытаемся разложить на множители каждый из терминов, найденных на первом этапе. Это продолжается до тех пор, пока мы больше не сможем принимать во внимание факторы. Когда мы больше не сможем разложить на множители, мы скажем, что многочлен полностью разложен на множители.2} + 4} \ right) \ left ({x + 2} \ right) \ left ({x — 2} \ right) \] Цель этого раздела — познакомиться со многими методами разложения многочленов на множители. Первый метод разложения многочленов — это разложение на множители наибольшего общего множителя . Чтобы использовать этот метод, все, что мы делаем, — это просматриваем все термины и определяем, есть ли фактор, общий для всех терминов.Если есть, мы вычленим его из полинома. Также обратите внимание, что в этом случае мы действительно используем только закон распределения в обратном порядке. Помните, что согласно закону о распределении доходов Выделяя наибольший общий множитель, мы делаем это в обратном порядке. Мы замечаем, что в каждом члене есть \ (a \), и поэтому мы «факторизуем» его, используя закон распределения в обратном порядке: Давайте рассмотрим несколько примеров.5} — 3x + 1} \ right) \] Обратите внимание на «+1», где 3 \ (x \) изначально было в последнем члене, поскольку последний член был термином, который мы вычленили, нам нужно было напомнить себе, что изначально там был термин. Одна из наиболее распространенных ошибок, связанных с этим типом задач факторинга, — это забыть об этой «1».2} + 6 \) Показать решение У этого термина также есть «-» перед третьим членом, как мы видели в предыдущей части. Однако на этот раз перед четвертым членом стоит знак «+», в отличие от последней части. Мы по-прежнему будем вычеркивать «-» при группировке, чтобы убедиться, что мы не теряем его из виду. Когда мы выносим за скобки «-», обратите внимание, что нам нужно заменить «+» в четвертом члене на «-». Опять же, вы всегда можете проверить, что это было сделано правильно, умножив «-» на круглые скобки.3} — 2} \ right) \] Факторинг по группировке может быть приятным, но срабатывает не так уж часто. Во-первых, отметим, что квадратичный — это еще один термин, обозначающий многочлен второй степени. Итак, мы знаем, что наибольший показатель квадратичного многочлена будет равен 2.{2} \), и единственный способ добиться этого — это умножить \ (x \) на \ (x \). Следовательно, первый член в каждом множителе должен быть \ (x \). Чтобы закончить это, нам просто нужно определить два числа, которые должны стоять на пустых местах. Мы можем значительно сузить возможности. После умножения двух множителей эти два числа нужно будет умножить, чтобы получить -15. Другими словами, эти два числа должны быть множителями -15. Вот все возможные способы множителя -15, используя только целые числа. Теперь мы можем просто вставить их один за другим и умножать, пока не получим правильную пару. Однако есть еще одна хитрость, которую мы можем использовать здесь, чтобы помочь нам. Чтобы получить коэффициент при члене \ (x \), необходимо сложить правильную пару чисел.2} \) означает умножение 3 \ (x \) и \ (x \), это должны быть первые два члена. Однако найти числа для двух пробелов будет не так просто, как в предыдущих примерах. Нам нужно будет начать со всеми множителями -8. На данный момент единственный вариант — выбрать пару, подключить их и посмотреть, что произойдет, когда мы умножим члены. Итак, мы получили.2} — 17x + 6 = \ left ({5x + \ underline {\, \, \, \,}} \ right) \ left ({x + \ underline {\, \, \, \,}} \ right ) \] Далее нам нужны все множители 6. Вот они. Не забывайте о негативных факторах. Часто именно они нам и нужны. Фактически, заметив, что коэффициент при \ (x \) отрицателен, мы можем быть уверены, что нам понадобится одна из двух пар отрицательных факторов, поскольку это будет единственный способ получить там отрицательный коэффициент.2} + 10x — 6 & = \ left ({2x + \ underline {\, \, \, \,}} \ right) \ left ({2x + \ underline {\, \, \, \,}} \ вправо) \ end {align *} \] Чтобы заполнить пробелы, нам понадобятся все множители -6. Также обратите внимание, что на этапе проб и ошибок мы должны убедиться и включить каждую пару в обе возможные формы и в оба возможных порядка, чтобы правильно определить, является ли это правильной парой факторов или нет.2} \] Это просто неверно для подавляющего большинства сумм квадратов, поэтому будьте осторожны, чтобы не совершить эту очень распространенную ошибку. Есть редкие случаи, когда это можно сделать, но ни один из этих особых случаев здесь не рассматривается. В целом не существует единого метода для этого. Однако есть некоторые, что мы можем сделать, поэтому давайте рассмотрим несколько примеров. Обратите внимание, что это преобразование в \ (u \) вначале может быть полезно в некоторых случаях, однако, как только вы к этому привыкнете, это обычно происходит в наших головах. Мы не сделали здесь много задач и не рассмотрели все возможности. Тем не менее, мы рассмотрели некоторые из наиболее распространенных приемов, с которыми мы можем столкнуться в других главах этой работы. Есть ли у вас представление о факторизации многочленов ? Поскольку теперь у вас есть основная информация о многочленах, мы узнаем, как решать квадратичные многочлены с помощью факторизации. Прежде всего, давайте быстренько рассмотрим квадратное уравнение . Квадратное уравнение — это многочлен второй степени, обычно в форме f (x) = ax 2 + bx + c, где a, b, c, ∈ R, и a ≠ 0. Термин «a» означает называется старшим коэффициентом, а «c» — абсолютным членом f (x). Каждое квадратное уравнение имеет два значения неизвестной переменной, обычно называемых корнями уравнения (α, β). По этой причине факторизация является фундаментальным шагом на пути к решению любого уравнения в математике. Давайте разберемся. Факторинг квадратного уравнения можно определить как процесс разбиения уравнения на произведение его факторов. Другими словами, мы также можем сказать, что факторизация — это обратное умножению. Для решения квадратного уравнения ax 2 + bx + c = 0 путем факторизации используются следующие шаги : Пример 1 Решите: 2 (x 2 + 1) = 5x Решение Разверните уравнение и переместите все члены слева от знака равенства. ⟹ 2x 2 — 5x + 2 = 0 ⟹ 2x 2 — 4x — x + 2 = 0 ⟹ 2x (x — 2) — 1 (x — 2) = 0 ⟹ ( x — 2) (2x — 1) = 0 Приравняем каждый множитель к нулю и решим ⟹ x — 2 = 0 или 2x — 1 = 0 ⟹ x = 2 или x = 1212 Следовательно, решения x = 2, 1/2. Пример 2 Решить 3x 2 — 8x — 3 = 0 Решение 3x 2 — 9x + x — 3 = 0 ⟹ 3x (x — 3) + 1 (x — 3) = 0 ⟹ (x — 3) (3x + 1) = 0 ⟹ x = 3 или x = -13 Пример 3 Решите следующее квадратное уравнение ( 2x — 3) 2 = 25 Решение Разверните уравнение (2x — 3) 2 = 25, чтобы получить; ⟹ 4x 2 — 12x + 9-25 = 0 ⟹ 4x 2 — 12x — 16 = 0 Разделите каждый член на 4, чтобы получить; ⟹ x 2 — 3x — 4 = 0 ⟹ (x — 4) (x + 1) = 0 ⟹ x = 4 или x = -1 Существует множество методов факторизации квадратных уравнений. Таким образом, мы будем использовать метод проб и ошибок, чтобы получить правильные множители. для данного квадратного уравнения. Чтобы разложить квадратное уравнение вида x 2 + bx + c, старший коэффициент равен 1. Вам необходимо определить два числа, произведение и сумма которых равны c и b соответственно. СЛУЧАЙ 1: Когда b и c положительны Пример 4 Решите квадратное уравнение: x 2 + 7x + 10 = 0 Перечислите множители 10: 1 × 10, 2 × 5 Определите два множителя с произведением 10 и суммой 7: 1 + 10 ≠ 7 Проверьте множители, используя свойство распределения умножения. (x + 2) (x + 5) = x 2 + 5x + 2x + 10 = x 2 + 7x + 10 Факторы квадратного уравнения: (x + 2) (x + 5) Приравнивание каждого множителя к нулю дает; x + 2 = 0 ⟹x = -2 x + 5 = 0 ⟹ x = -5 Следовательно, решение x = — 2, x = — 5 Пример 5 х 2 + 10х + 25. Решение Определите два фактора с произведением 25 и суммой 10. 5 × 5 = 25 и 5 + 5 = 10 Проверьте факторы. x 2 + 10x + 25 = x 2 + 5x + 5x + 25 = x (x + 5) + 5x + 25 = x (x + 5) + 5 (x + 5) = (x + 5) (x + 5) Следовательно, x = -5 — это ответ. СЛУЧАЙ 2: Когда b положительно, а c отрицательно Пример 6 Решите x 2 + 4x — 5 = 0 Решение Запишите множители -5. 1 × –5, –1 × 5 Определите факторы, произведение которых равно — 5, а сумма равна 4. 1 — 5 ≠ 4 Проверьте факторы, используя свойство распределения. (x — 1) (x + 5) = x 2 + 5x — x — 5 = x 2 + 4x — 5 x — 1 = 0 ⇒ x = 1 или Следовательно, x = 1, x = -5 — решения. СЛУЧАЙ 3: Когда b и c отрицательны Пример 7 x 2 — 5x — 6 Решение Запишите множители — 6: 1 × –6, –1 × 6, 2 × –3, –2 × 3 Теперь определите факторы, произведение которых равно -6, а сумма равна –5: 1 + (–6) = –5 Проверьте коэффициенты используя распределительное свойство. (x + 1) (x — 6) = x 2 — 6 x + x — 6 = x 2 — 5x — 6 Приравняйте каждый множитель к нулю и решите, чтобы получить; x + 1 = 0 ⇒ x = -1, или Следовательно, решение x = 6, x = -1 СЛУЧАЙ 4: Когда b отрицательно, а c положительно Пример 8 x 2 — 6x + 8 = 0 Решение Запишите все множители 8 . –1 × — 8, –2 × –4 Определите факторы, произведение которых равно 8, а сумма равна -6 Проверьте коэффициенты с помощью распределительного свойства. (x — 2) (x — 4) = x 2 — 4 x — 2x + 8 = x 2 — 6x + 8 Теперь приравняйте каждый множитель к нулю и решите выражение, чтобы получить; (x — 2) (x — 4) = 0 x — 2 = 0 ⇒ x = 2 или Пример 9 Разложить на множители x 2 + 8x + 12. Решение Запишите множители 12; 12 = 2 × 6 или = 4 × 3 2 + 6 = 8 Используйте свойство распределения, чтобы проверить множители; = x 2 + 6x + 2x + 12 = (x 2 + 6x) + (2x + 12) = x (x + 6) +2 (x + 6) = x (x + 6 ) +2 (x + 6) = (x + 6) (x + 2) Приравняем каждый множитель к нулю, чтобы получить; (x + 6) (x + 2) x = -6, -2 Иногда старший коэффициент квадратного уравнения может быть больше чем 1.В этом случае мы не можем решить квадратное уравнение, используя общие множители. Следовательно, нам нужно рассмотреть коэффициент при x 2 и множители при c, чтобы найти числа, сумма которых равна b. Пример 10 Решите 2x 2 — 14x + 20 = 0 Решение Определите общие множители уравнения. 2x 2 — 14x + 20 ⇒ 2 (x 2 — 7x + 10) Теперь мы можем найти множители (x 2 — 7x + 10).Поэтому запишите коэффициенты 10: –1 × –10, –2 × –5 Определите коэффициенты, сумма которых равна — 7: 1 + (–10) ≠ –7 Проверьте коэффициенты, применив свойство распределения. 2 (x — 2) (x — 5) = 2 (x 2 — 5 x — 2x + 10) Приравняйте каждый множитель к нулю и решите; x — 2 = 0 ⇒ x = 2 или Пример 11 Решить 7x 2 + 18x + 11 = 0 Решение Запишите множители 7 и 11. 7 = 1 × 7 11 = 1 × 11 Примените свойство распределения для проверки факторов, как показано ниже: (7x + 1) (x + 11) ≠ 7x 2 + 18x + 11 (7x + 11) (x + 1) = 7x 2 + 7x + 11x + 11 = 7x 2 + 18x + 11 Теперь приравняйте каждый множитель к нулю и решите, чтобы получить; 7x 2 + 18x + 11 = 0 x = -1, -11/7 Пример 12 Решить 2x 2 — 7x + 6 = 3 Решение 2x 2 — 7x + 3 = 0 (2x — 1) (x — 3) = 0 x = 1/2 или x = 3 Пример 13 Решить 9x 2 + 6x + 1 = 0 Решение Разложите на множители, чтобы получить: (3x + 1) (3x + 1) = 0 (3x + 1) = 0, Следовательно, x = −1 / 3 Пример 14 Разложить на множители 6x 2 — 7x + 2 = 0 Решение 6x 2 — 4x — 3x + 2 = 0 Разложите выражение на множители; ⟹ 2x (3x — 2) — 1 (3x — 2) = 0 ⟹ (3x — 2) (2x — 1) = 0 ⟹ 3x — 2 = 0 или 2x — 1 = 0 ⟹ 3x = 2 или 2x = 1 ⟹ x = 2/3 или x = ½ Пример 15 Факторизация x 2 + (4 — 3y) x — 12y = 0 Решение Разверните уравнение; x 2 + 4x — 3xy — 12y = 0 Разложить на множители; ⟹ x (x + 4) — 3y (x + 4) = 0 x + 4) (x — 3y) = 0 ⟹ x + 4 = 0 или x — 3y = 0 ⟹ x = -4 или x = 3y Таким образом, x = -4 или x = 3y Решите следующие квадратные уравнения путем факторизации: Ответы Квадратное уравнение это
многочлен
уравнение
степень
2
. 0
знак равно
а
Икс
2
+
б
Икс
+
c куда
а
,
б
а также
c
все реальные числа и
а
≠
0
. Если мы заменим
0
с участием
у
, то получаем
квадратичная функция у
знак равно
а
Икс
2
+
б
Икс
+
c чей график будет
парабола
. Точки пересечения графика
Икс
-оси будут решениями уравнения,
а
Икс
2
+
б
Икс
+
c
знак равно
0
. То есть, если многочлен
а
Икс
2
+
б
Икс
+
c
может быть учтен на
(
Икс
—
п
)
(
Икс
—
q
)
, мы знаем по
свойство нулевого продукта
что если
(
Икс
—
п
)
(
Икс
—
q
)
знак равно
0
, или
(
Икс
—
п
)
знак равно
0
или
(
Икс
—
q
)
знак равно
0
. Поскольку
Икс
-координата
вершина параболы
это точно середина
Икс
-перехватывает
, то
Икс
-координата вершины будет
п
+
q
2
. Вы можете использовать
Икс
-координата вершины для нахождения
у
-координат. Теперь у вас есть вершина и
2
другие точки параболы (а именно,
Икс
-перехватывает). Вы можете использовать эти три точки для построения графика. Пример 1: Постройте график функции
у
знак равно
Икс
2
—
8
Икс
+
12
с использованием факторинга. Сравните уравнение со стандартной формой,
у
знак равно
а
Икс
2
+
б
Икс
+
c
. Поскольку значение
а
положительный, парабола открывается. Разложите на множители трехчлен,
Икс
2
—
8
Икс
+
12
. Идентифицировать
2
числа, сумма которых
—
8
и продукт
12
.Цифры
—
2
а также
—
6
. То есть,
Икс
2
—
8
Икс
+
12
знак равно
(
Икс
—
2
)
(
Икс
—
6
)
. Икс
2
—
8
Икс
+
12
знак равно
0
⇒
(
Икс
—
2
)
(
Икс
—
6
)
знак равно
0 Итак, по свойству нулевого продукта либо
(
Икс
—
2
)
знак равно
0
или
(
Икс
—
6
)
знак равно
0
. Следовательно
Икс
-перехваты функции
6
а также
2
. В
Икс
-координата вершины — это середина х-точек пересечения. Итак, вот
Икс
-координата вершины будет
2
+
6
2
знак равно
4
. Заменять
Икс
знак равно
4
в уравнении
у
знак равно
Икс
2
—
8
Икс
+
12
найти
у
-координата вершины. у
знак равно
(
4
)
2
—
8
(
4
)
+
12
знак равно
16
—
32
+
12
знак равно
—
4 То есть координаты вершины равны
(
4
,
—
4
)
. Теперь у нас 3 очка
(
4
,
—
4
)
,
(
2
,
0
)
а также
(
6
,
0
)
которые находятся на параболе. Нанесите точки. Соедините их плавной кривой и продолжите параболу. Пример 2: Постройте график функции
у
знак равно
—
Икс
2
—
2
Икс
+
8
с использованием факторинга. Сравните уравнение со стандартной формой,
у
знак равно
а
Икс
2
+
б
Икс
+
c
. Поскольку значение
а
положительный, парабола открывается. Разложите на множители трехчлен,
—
Икс
2
—
2
Икс
+
8
. Во-первых, фактор вне
—
1
. —
Икс
2
—
2
Икс
+
8
знак равно
—
1
(
Икс
2
+
2
Икс
—
8
) Разложите выражение на множители в скобках. Идентифицировать
2
числа, сумма которых
2
и продукт
—
8
.Цифры
4
а также
—
2
. То есть,
Икс
2
+
2
Икс
—
8
знак равно
(
Икс
+
4
)
(
Икс
—
2
)
. Тогда данная функция принимает вид
у
знак равно
—
(
Икс
+
4
)
(
Икс
—
2
)
. Так,
у
знак равно
0
следует из свойства нулевого продукта,
Икс
+
4
знак равно
0
или
Икс
—
2
знак равно
0
. Следовательно
Икс
-перехваты графика
—
4
а также
2
. В
Икс
-координата вершины параболы — середина
Икс
-перехватывает.Итак, вот
Икс
-координата вершины будет
—
4
+
2
2
знак равно
—
1
. Заменять
Икс
знак равно
—
1
в уравнении
у
знак равно
—
Икс
2
—
2
Икс
+
8
найти
у
-координата вершины. у
знак равно
—
(
—
1
)
2
—
2
(
—
1
)
+
8
знак равно
—
1
+
2
+
8
знак равно
9 Итак, координаты вершины равны
(
—
1
,
9
)
. Теперь у нас есть
3
точки
(
—
1
,
9
)
,
(
—
4
,
0
)
а также
(
2
,
0
)
которые находятся на параболе. Наибольший общий фактор
 При факторинге в целом это также будет первое, что мы должны попробовать, поскольку это часто упрощает проблему.
При факторинге в целом это также будет первое, что мы должны попробовать, поскольку это часто упрощает проблему. Для этого нам понадобится «+1» и обратите внимание, что это «+1» вместо «-1», потому что термин изначально был положительным. Если бы изначально это был отрицательный термин, нам пришлось бы использовать «-1».
Для этого нам понадобится «+1» и обратите внимание, что это «+1» вместо «-1», потому что термин изначально был положительным. Если бы изначально это был отрицательный термин, нам пришлось бы использовать «-1». Обратите внимание, что, как мы видели в последних двух частях этого примера, если перед третьим членом стоит «-», мы часто также вычленяем его из третьего и четвертого терминов, когда мы их группируем.
Обратите внимание, что, как мы видели в последних двух частях этого примера, если перед третьим членом стоит «-», мы часто также вычленяем его из третьего и четвертого терминов, когда мы их группируем. Разложение квадратичных многочленов на множители

 2} + 2x — 8 \]
2} + 2x — 8 \] 2} + 10x — 6 = \ left ({2x — 1} \ right) \ left ({2x + 6} \ right) \]
2} + 10x — 6 = \ left ({2x — 1} \ right) \ left ({2x + 6} \ right) \] Факторинговые многочлены со степенью больше 2

Факторинговые квадратные уравнения — методы и примеры
 Мы можем получить корни квадратного уравнения, разложив уравнение на множители.
Мы можем получить корни квадратного уравнения, разложив уравнение на множители. Как разложить квадратное уравнение на множители?
 В этой статье мы сделаем акцент на том, как разложить квадратные уравнения на множители, в которых коэффициент при x 2 равен 1 или больше 1.
В этой статье мы сделаем акцент на том, как разложить квадратные уравнения на множители, в которых коэффициент при x 2 равен 1 или больше 1. Факторинг, когда коэффициент x
2 равен 1
2 + 5 = 7.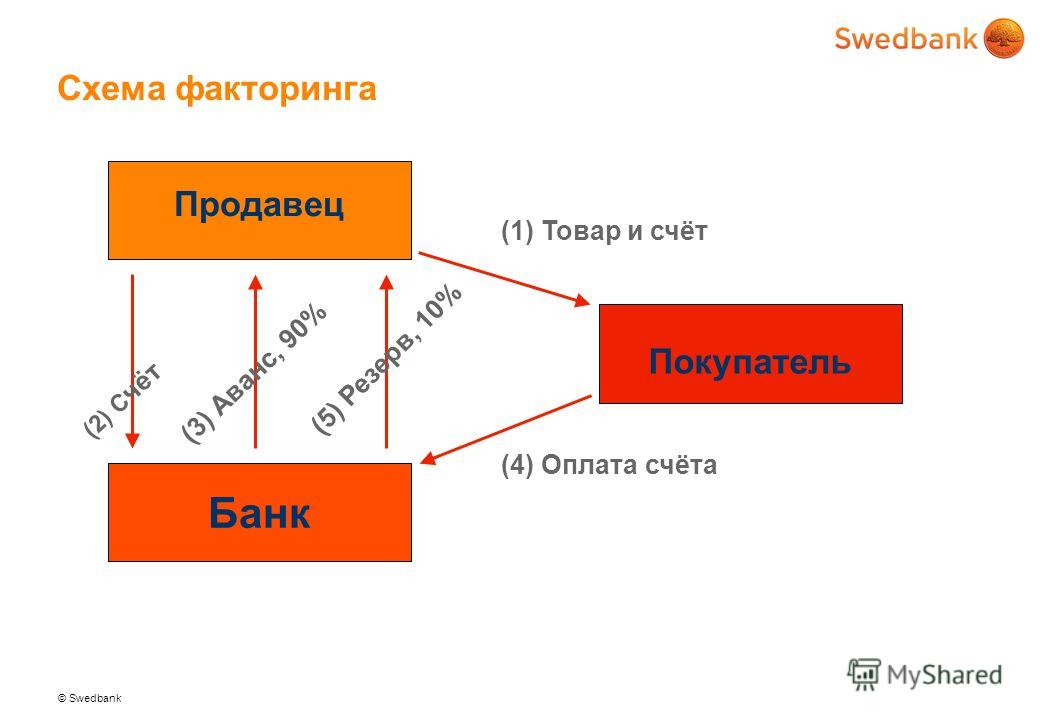
–1 + 5 = 4
(x — 1) (x + 5) = 0
x + 5 = 0 ⇒ x = -5
(x + 1) (x — 6) = 0
x — 6 = 0 ⇒ x = 6
–1 + (–8) ≠ –6
–2 + (–4) = –6
x — 4 = 0 ⇒ x = 4
Найдите множители, сумма которых равна 8:
2 × 6 ≠ 8 Факторинг, когда коэффициент x
2 больше 1
–2 + (–5) = –7
= 2 (x 2 — 7x + 10) = 2x 2 — 14x + 20
2 (x — 2) (x — 5) = 0
x — 5 = 0 ⇒ x = 5
(7x + 11) (x + 1) = 0
Предыдущий урок | Главная страница | Следующий урок Построение графиков квадратных уравнений с использованием факторинга
 Стандартная форма квадратного уравнения:
Стандартная форма квадратного уравнения: потом
п
а также
q
являются решениями уравнения
а
Икс
2
+
б
Икс
+
c
знак равно
0
и поэтому
Икс
-перехваты квадратного уравнения.
потом
п
а также
q
являются решениями уравнения
а
Икс
2
+
б
Икс
+
c
знак равно
0
и поэтому
Икс
-перехваты квадратного уравнения.
 Тогда корни уравнения равны
2
а также
6
.
Тогда корни уравнения равны
2
а также
6
.


 Нанесите точки. Соедините их плавной кривой и продолжите параболу.
Нанесите точки. Соедините их плавной кривой и продолжите параболу. Факторинговые многочлены
Факторинг, процесс «неумножения» многочленов с целью возврата к уникальной строке многочленов меньшей степени, произведение которых является исходным многочленом, является самым простым способом решения уравнений более высокой степени.Хотя вы уже должны хорошо разбираться в факторинге, вот методы, с которыми вам следует ознакомиться на случай, если вам понадобится обзор. Наибольшие общие факторы
Если все члены полинома содержат один или несколько идентичных множителей, объедините эти похожие множители в один моном, называемый наибольшим общим множителем , и перепишите полином в факторизованной форме.
Пример 1: Разложите выражения на множители.
15 x 3 + 5 x 2 −25 x
Поскольку каждый член полинома делится как на x , так и на 5, наибольший общий делитель равен 5 x .
В факторизованной форме многочлен записывается как 5 x (3 x 2 + x — 5).
18 x 3 y 5 z 4 + 6 x 2 yz 3 — 9 x 2 y
8 3 z 2Наибольший моном, на который каждый из членов делится без остатка, таким образом, наибольший общий делитель, равен 3 x 2 yz 2 , поэтому вычтите его за множитель.
Факторинг по группировке
Иногда наибольший общий фактор выражения — это не просто одночлен, а целая величина в скобках. Вам разрешено вычитать количества в скобках так же, как вы можете вычитать отдельные термины.
Пример 2: Разложите следующие выражения на множители.
3 x ( x — 5) + 2 y ( x — 5) — 10 ( x — 5)
Единственное, что делится на каждый из этих членов равномерно, — это линейное выражение ( x — 5).Вынесите его за скобки, как если бы вы делали любой наибольший общий множитель, оставив одночлен в каждом члене, умноженном на ( x — 5):
3 x 2 — 6 x — 4 x + 8
Ничто, кроме числа 1, не делится равномерно на каждое из членов, и нет смысла вычитать 1. Однако первые два члена имеют наибольший общий множитель 3 x . Кроме того, если вынести -4 из последних двух членов, вы можете разложить их по группам:
Факторинг квадратичных трехчленов
Ваша самая распространенная задача разложения на множители, помимо наибольшего общего разложения, — это преобразование квадратного трехчлена в произведение двух линейных биномов.
Пример 3: Разложите следующие выражения на множители.
x 2 — 4 x — 12
Если ведущий коэффициент равен 1, как здесь, процесс прост. Найдите два числа, сумма которых равна коэффициенту при члене x , а произведение которых равно постоянному члену. Единственные два числа, сумма которых равна −4 и которые умножаются, чтобы дать −12, — это −6 и 2. Используйте их как константы в линейных множителях:
x 2 -10 x + 24
Так как этот квадратный трехчлен имеет старший коэффициент 1, найдите два числа с произведением 24 и суммой −10.Поэкспериментировав, вы обнаружите, что эти числа равны −6 и −4:
.
2 x 2 + 9 x — 5
Если ведущий коэффициент не равен 1, необходимо выполнить другую процедуру. Вы по-прежнему ищете два числа, и эти числа все равно дадут в сумме 9. Однако они умножатся и вы получите −10, произведение ведущего коэффициента и константы. (Вам не нужно было использовать эту технику, когда ведущий коэффициент был равен 1, поскольку произведение ведущего коэффициента и константы в любом случае было бы константой.) Рассматриваемые числа — 10 и -1. Перепишите коэффициент x как сумму этих чисел:
Распределите x как на 10, так и на −1:
До финиша, фактор по группировке:
Шаблоны специальных коэффициентов
Иногда единственное усилие, которое вам придется приложить для решения проблемы факторизации, — это признать, что рассматриваемый многочлен соответствует одному из трех конкретных шаблонов.Вам следует запомнить каждую из этих формул, чтобы сразу их заметить:
- Разница полных квадратов: x 2 — a 2 = ( x + a ) ( x — a )
- Разница идеальных кубов: a 3 — b 3 = ( a xs — b ) ( a 2 + ab + b 2 )
- Сумма идеальных кубов: a 3 + b 3 = ( a + b ) ( a 2 — ab + b 2 )
Пример 4: Полностью разложите следующие выражения на множители.
27 x 3 + 8
Обратите внимание, что 27 x 3 и 8 являются идеальными кубами, поэтому примените формулу суммы идеальных кубов:
20 x 2 -405
Похоже, это не соответствует ни одному из шаблонов, но для начала вы можете вычесть наибольший общий множитель 5:
Теперь более ясно, что (4 x 2 — 81) является разностью полных квадратов, поскольку (2 x ) 2 = 4 x 2 и 9 2 = 81:
факторинговых многочленов: практические инструкции | Purplemath
Purplemath
Как указывалось на предыдущей странице, синтетическое деление можно использовать для проверки того, является ли данное значение x нулем полиномиальной функции (путем возврата нулевого остатка), а также его можно использовать для деления линейного множителя. от этого многочлена (оставляя один с многочленом меньшей степени).
Из-за этой тесной связи между нулями (полиномиальных функций) и решениями (полиномиальных уравнений) методы, используемые для «решения» полиномов, могут быть одинаково хорошо применены для нахождения полной факторизации полинома.
MathHelp.com
Основное различие между упражнениями «решение» на предыдущей странице и упражнениями «факторинг» на этой странице состоит в том, что для факторинга мы должны отслеживать любые числа, которые мы делим.Примером этого может быть 2, которые я выделил из квадратичной в конце примера на предыдущей странице. Когда мы решаем «(многочлен) равен нулю», нас не заботит, действительно ли на каком-то этапе уравнение было «2 × (многочлен) равен нулю». Но, что касается факторинга, мы заботимся об этих начальных 2.
Кроме того, когда мы выполняем упражнения по факторингу, нам может потребоваться использовать формулы разности или суммы кубов для некоторых упражнений. Это менее распространено при решении.
С другой стороны, полиномы для упражнений на «факторизацию» обычно включают более точные числа, без значений комплексных чисел или беспорядочных квадратных корней, характерных для упражнений «решение».
Полностью множитель: 30
x 5 — 166 x 4 — 542 x 3 + 2838 x 2 + 1520 x — 800
Все коэффициенты четные, так что я могу вынести 2 сразу. Но это не уравнение «равно нулю», поэтому я не могу просто «разделить» 2, чтобы оно исчезло.Вместо этого мне придется не забыть включить множитель 2 в мою окончательную формулировку факторинга.
На данный момент у меня есть следующее:
2 (15 x 5 -83 x 4 -271 x 3 + 1419 x 2 + 760 x -400)
Даже после того, как отложил 2, я все еще застрял с некоторыми довольно большими числами:
15 x 5 -83 x 4 -271 x 3 + 1419 x 2 + 760 x -400
Тест рациональных корней дал мне ошеломляюще длинный список возможных корней, включая множество дробей.По крайней мере, сначала я буду придерживаться целочисленного множителя, равного 400. Я выясню весь длинный список позже — если потребуется.
Поскольку решения многочленов обычно довольно «близки к середине», я не буду утруждать себя тестированием решений типа x = 400 в моем синтетическом подразделении, по крайней мере, на начальном этапе. Вместо этого я буду стараться делать первые предположения небольшими.
Но прежде чем я начну гадать, я проверим график:
Похоже, что –4 и 5 были бы отличным первым выбором для моего синтетического дивизиона.График при x = 5 отскакивает от оси, поэтому я предполагаю, что это повторяющийся корень. Сначала я попробую синтетический дивизион, а потом попробую дважды:
Итак, я вытащил две копии множителя x — 5. Я знаю взятые множители; последняя строка синтетического деления выше говорит мне, что мой полином теперь:
2 ( x — 5) 2 (15 x 3 + 67 x 2 + 24 x — 16)
Часть выражения, которую я оставил для разложения, — это кубика в последних скобках выше.(Откуда я узнал, что это кубик? Потому что мне дали что-то пятой степени, и я вычеркнул два линейных множителя.)
Филиал
Чтобы проверить свою работу (и подтвердить идентичность последнего «хорошего» нуля), я построю график полиномиальной функции, связанной с оставшимся кубическим фактором, равным 15 x 3 + 67 x 2 + 24 x — 16:
Итак, похоже, что x = –4 — все еще значение, которое я хочу проверить.Вот мое синтетическое подразделение:
Я был прав; x = –4 — ноль. Если вычесть коэффициент x + 4, у меня останется только квадратичный коэффициент:
Я могу использовать обычные методы факторинга, чтобы завершить факторинг:
15 x 2 + 7 x — 4 = (5 x + 4) (3 x — 1)
(Между прочим, эти два фактора создали два «беспорядочных» корня на графике:
–4/5 и 1/3.)Теперь мне нужно вернуться к своей работе и собрать все мои факторы, начиная с первых двух, которые я исключил. Моя полная факторизация:
2 ( x — 5) 2 ( x + 4) (5 x + 4) (3 x — 1)
В вашем практическом ответе факторы с переменными не обязательно должны быть перечислены в каком-либо определенном порядке, поскольку порядок не имеет значения для умножения.Но любой постоянный член, такой как «2», должен идти впереди. И многие книги предпочитают записывать повторяющиеся множители в экспоненциальной форме, например «( x — 5) 2 » в моем окончательном ответе выше.
Между прочим, если у вас нет графического калькулятора, вам предстоит нелегкая дорога. Чтобы ответить на эти вопросы о факторинге, вы захотите начать с Rational Roots Test. Работая со списком, предоставленным тестом, вы захотите начать тестирование меньших целочисленных значений, обычно являющихся факторами постоянного члена, и работать оттуда.
Имейте в виду, что «решение» « x = a » означает, что у вас есть коэффициент « x — a ». Уберите все возможные множители и всегда продолжайте работу с тем, что остается меньшим и более простым полиномом. И сделайте быструю проверку, по крайней мере, нового постоянного члена, чтобы увидеть, есть ли тестовые значения, которые вы можете удалить по мере продвижения.
Вместо построения графиков есть уловка, которую вы можете использовать с синетическим делением, чтобы знать, когда прекратить переход к более высоким или более низким значениям теста.Кроме того, вам может быть полезно Правило знаков Декарта, поскольку оно может сказать вам о максимальном количестве положительных или отрицательных нулей, которые может иметь многочлен.
Я бы также посоветовал выполнять как можно больше практических задач, потому что, если вы серьезно потренировали эту конкретную ментальную мышцу, это может иметь большое значение в следующем тесте.
Полностью множитель: 3
x 6 -12 x 5 + 12 x 4 + 24 x 3 -96 x 2 + 96 x
Я могу вытащить не только тройку спереди, но и x .Это оставляет мне фактор:
x 5 — 4 x 4 + 4 x 3 + 8 x 2 -32 x + 32
Возможные нули полинома пятой степени (то есть степени пять) будут плюс и минус множители тридцати двух, или:
Я могу попробовать трюк, просто подключив его. x = –1:
–1 — 4 — 4 + 8 + 32 + 32 = 63
Даже близко нет.А как насчет x = 1?
1–4 + 4 + 8–32 + 32 = 9
Хорошо; Думаю, я попробую следующие большие возможности. А как насчет x = 2?
Наконец-то! Последняя строка выше говорит мне, что x = 2 — это ноль, поэтому ( x = 2) является множителем. Удалив этот фактор, у меня останется следующее:
Я заметил, что приведенные выше термины могут быть объединены в пары таким образом, чтобы я мог напрямую это учитывать:
( x 4 -2 x 3 ) + (8 x -16)
x 3 ( x -2) + 8 ( x -2)
( x -2) ( x 3 + 8)
Очевидно, x — 2 — еще один фактор.Итак, теперь я остался с кубиком. И это сумма кубов, поэтому я воспользуюсь этой формулой для завершения факторизации:
(Я помню, когда я узнал о суммах и разностях кубов, что квадратичный фактор не учитывается. Так что я знаю, что на этом закончил.)
Теперь я вернулся к началу и убедился, что уловил все факторы, которые вытащил на этом пути. Мой последний ответ:
3 x ( x — 2) 2 ( x + 2) ( x 2 -2 x + 4)
URL: https: // www.purplemath.com/modules/solvpoly2.htm
Факторинговые многочлены — алгебра и тригонометрия
Цели обучения
В этом разделе будут учащиеся:
- Разложите на множители наибольший общий делитель многочлена.
- Разложите на множители трехчлены.
- Фактор по группировке.
- Выложите множитель на множители полного квадрата.
- Выведите множитель разницы квадратов.
- Разложите множители на сумму и разность кубиков.
- Факторные выражения с использованием дробных или отрицательных степеней.
Представьте, что мы пытаемся найти площадь лужайки, чтобы определить, сколько семян травы нужно купить. Газон — это зеленая часть на (Рисунок).
Рисунок 1.Площадь всей области может быть найдена по формуле площади прямоугольника.
Площадь участков, не требующих семян травы, необходимо вычесть из площади всего региона.Каждая из двух квадратных областей имеет площадь единиц 2 . Другая прямоугольная область имеет одну сторону длины и одну сторону длины, что дает площадь единиц 2 . Таким образом, область, которую необходимо вычесть, имеет площадь единиц 2 .
Площадь области, требующей семян травы, находится с помощью единиц вычитания 2 . Эта площадь также может быть выражена в факторизованной форме как единицы 2 . Мы можем подтвердить, что это эквивалентное выражение, умножив.
Многие полиномиальные выражения могут быть записаны в более простой форме с помощью факторизации.В этом разделе мы рассмотрим различные методы, которые можно использовать для факторизации полиномиальных выражений.
Разложение на множители трехчлена идеального квадрата
Полный квадрат трехчлена — это трехчлен, который можно записать как квадрат двучлена. Напомним, что когда бином возводится в квадрат, результатом является квадрат первого члена, добавленный к удвоенному произведению двух членов и квадрата последнего члена.
Мы можем использовать это уравнение, чтобы разложить на множители любой трехчлен полного квадрата.
Трехчлены идеального квадрата
Полный квадрат трехчлена может быть записан как квадрат двучлена:
Как к
Разложите на множитель квадрата трехчлена на квадрат двучлена.
- Подтвердите, что первый и последний член являются точными квадратами.
- Подтвердите, что средний член в два раза больше произведения
- Запишите факторизованную форму как
Разложение на множители трехчлена идеального квадрата
Фактор
Попробуйте
Фактор
[show-answer q = ”fs-id11673392 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673392 ″]
[/ hidden-answer]
Факторизация квадратов
Разность квадратов — это полный квадрат, вычитаемый из полного квадрата.Напомним, что разность квадратов может быть переписана как множители, содержащие одинаковые члены, но противоположные знаки, потому что средние члены компенсируют друг друга при умножении двух множителей.
Мы можем использовать это уравнение, чтобы разложить на множители любые разности квадратов.
Различия квадратов
Разность квадратов можно переписать как два множителя, содержащих одинаковые члены, но противоположные знаки.
Как к
Разложите на разность квадратов на биномы.
- Подтвердите, что первый и последний член являются точными квадратами.
- Запишите факторизованную форму как
Факторизация квадратов
Фактор
Попробуйте
Фактор
[show-answer q = ”fs-id11673383 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
83 ″]
[/ hidden-answer]
Есть ли формула для разложения суммы квадратов на множители?
№Сумму квадратов нельзя разложить на множители.
Факторизация суммы и разности кубов
Теперь мы рассмотрим два новых специальных продукта: сумму и разность кубиков. Хотя сумма квадратов не может быть разложена на множители, сумма кубов может быть разложена на бином и трехчлен.
Точно так же сумму кубов можно разложить на двучлен и трехчлен, но с разными знаками.
Мы можем использовать аббревиатуру SOAP, чтобы запомнить знаки при разложении суммы или разности кубов.Первая буква каждого слова относится к знакам: S ame O pposite A lways P ositive. Например, рассмотрим следующий пример.
Знак первых 2 — это тот же , что и знак между. Знак термина напротив знак между И знак последнего члена, 4, всегда положительный .
Сумма и разность кубов
Сумму двух кубов можно разложить на
.Мы можем разложить два куба на множители как
.Как к
Сумма кубиков или разность кубов, умножьте ее на множители.
- Подтвердите, что первый и последний член являются кубиками, или
- Для суммы кубов запишите факторизованную форму как Для разности кубов запишите факторизованную форму как
Попробуйте
Вычислим сумму кубиков:
[show-answer q = ”fs-id1167339296456 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339296456 ″]
[/ hidden-answer]
Факторизация кубиков
Фактор
Анализ
Как и в случае с суммой кубиков, мы не сможем дополнительно разложить на множители трехчленную часть.
Попробуйте
Фактор разницы кубиков:
[show-answer q = ”fs-id11673313 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
13 ″]
[/ hidden-answer]
Ключевые уравнения
| разность квадратов | |
| полный квадрат трехчлен | |
| сумма кубиков | |
| разность кубиков |
- Наибольший общий множитель, или GCF, может быть выделен из полинома.Проверка GCF должна быть первым шагом в любой проблеме факторинга. См. (Рисунок).
- Трехчлены со старшим коэффициентом 1 можно разложить на множители, найдя числа, у которых есть произведение третьего члена и суммы второго члена. См. (Рисунок).
- Трехчлены можно разложить на множители с помощью процесса, называемого факторингом по группировке. См. (Рисунок).
- Трехчлены полного квадрата и разность квадратов являются специальными произведениями и могут быть разложены на множители с помощью уравнений. См. (Рисунок) и (Рисунок).
- Сумма кубиков и разность кубов можно разложить на множители с помощью уравнений. См. (Рисунок) и (Рисунок).
- Полиномы, содержащие дробные и отрицательные показатели степени, можно разложить на множители, вытащив GCF. См. (Рисунок).
Устный
Если члены многочлена не имеют ОКФ, означает ли это, что его нельзя факторизовать? Объяснять.
[show-answer q = ”fs-id11673327 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673327 ″]
Члены многочлена не обязательно должны иметь общий множитель, чтобы весь многочлен мог быть факторизован.Например, и не имеют общего множителя, но весь многочлен можно факторизовать:
[/ hidden-answer]
Многочлен факторизован, но не является трехчленом в виде полного квадрата или разностью двух квадратов. Можете ли вы разложить полином на множители, не найдя ОКФ?
Как вы учитываете при группировке?
[show-answer q = ”fs-id11673317 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
17 ″]
Разделите член на сумму двух членов, разложите на множители каждую часть выражения по отдельности, а затем вычтите фактор GCF всего выражения.
[/ hidden-answer]
Алгебраические
Найдите наибольший общий множитель для следующих упражнений.
[show-answer q = ”fs-id11673341 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
41 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339426591 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339426591 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673374 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
74 ″]
[/ hidden-answer]
Для следующих упражнений разбейте на группы.
[show-answer q = ”fs-id11673355 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673355 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673392 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
92 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339303632 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339303632 ″]
[/ hidden-answer]
Для следующих упражнений разложите многочлен на множители.
[show-answer q = ”fs-id11673345 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673345 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673362 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
62 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339321437 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339321437 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339344451 ″] Показать решение [/ show-answer][hidden-answer a = ”fs-id1167339344451 ″]
[/ hidden-answer] [show-answer q = ”fs-id1167339344556 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id1167339344556 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673373 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673373 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673318 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673318 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673354 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673354 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673362 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
62 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673368 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673368 ″]
[/ hidden-answer]
Для следующих упражнений разложите многочлены на множители.
[show-answer q = ”fs-id11673370 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673370 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673311 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673311 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673336 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673336 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673304 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
04 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673326 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id116733
26 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339317822 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339317822 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339438041 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339438041 ″]
[/ hidden-answer]
Реальные приложения
Для следующих упражнений рассмотрите следующий сценарий:
Шарлотта назначила председателя для руководства проектом благоустройства города.Первый акт — установка статуй и фонтанов в одном из парков города. Парк представляет собой прямоугольник площадью 2 , как показано на рисунке ниже. Длина и ширина парка являются идеальными факторами площади.
Разложите множители по группам, чтобы найти длину и ширину парка.
[show-answer q = ”fs-id1167339315871 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339315871 ″]
[/ hidden-answer]
В центре парка будет поставлена статуя.Площадь основания статуи равна площади, чтобы найти длины сторон статуи.
В северо-западном углу парка город собирается установить фонтан. Площадь основания фонтана равна площади, чтобы найти длины сторон фонтана.
[show-answer q = ”fs-id11673352 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673352 ″]
[/ hidden-answer]
Для следующего упражнения рассмотрим следующий сценарий:
Школа устанавливает флагшток на центральной площади.Площадь представляет собой квадрат со стороной 100 ярдов. как показано на рисунке ниже. Флагшток займет квадратный участок площадью 2 .
Найдите длину основания флагштока на множители.
Расширения
Для следующих упражнений разложите многочлены на множители полностью.
[show-answer q = ”fs-id11673313 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673313 ″]
[/ hidden-answer]
[show-answer q = ”fs-id11673353 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id11673353 ″]
[/ hidden-answer]
[show-answer q = ”fs-id1167339433090 ″] Показать решение [/ show-answer][скрытый-ответ a = ”fs-id1167339433090 ″]
[/ hidden-answer]
Глоссарий
- фактор путем группировки
- метод факторизации трехчлена в форме: деление члена x на сумму двух членов, факторизацию каждой части выражения отдельно, а затем разложение GCF всего выражения
- наибольший общий делитель
- наибольший многочлен, который без остатка делится на каждый многочлен
 Бизнес-Блог Блоготей Бизнес-Блог «Блоготей» — информационный блог о бизнесе и финансах. Полезные статьи и новости из мира бизнеса, финансов, банков, экономики, инвестиций.
Бизнес-Блог Блоготей Бизнес-Блог «Блоготей» — информационный блог о бизнесе и финансах. Полезные статьи и новости из мира бизнеса, финансов, банков, экономики, инвестиций. 
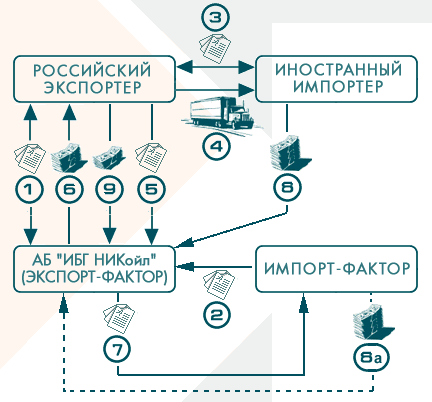
 Покупатель выплачивает деньги поставщику, который расплачивается с фактором.
Покупатель выплачивает деньги поставщику, который расплачивается с фактором.

 Москва)
Москва) 35
35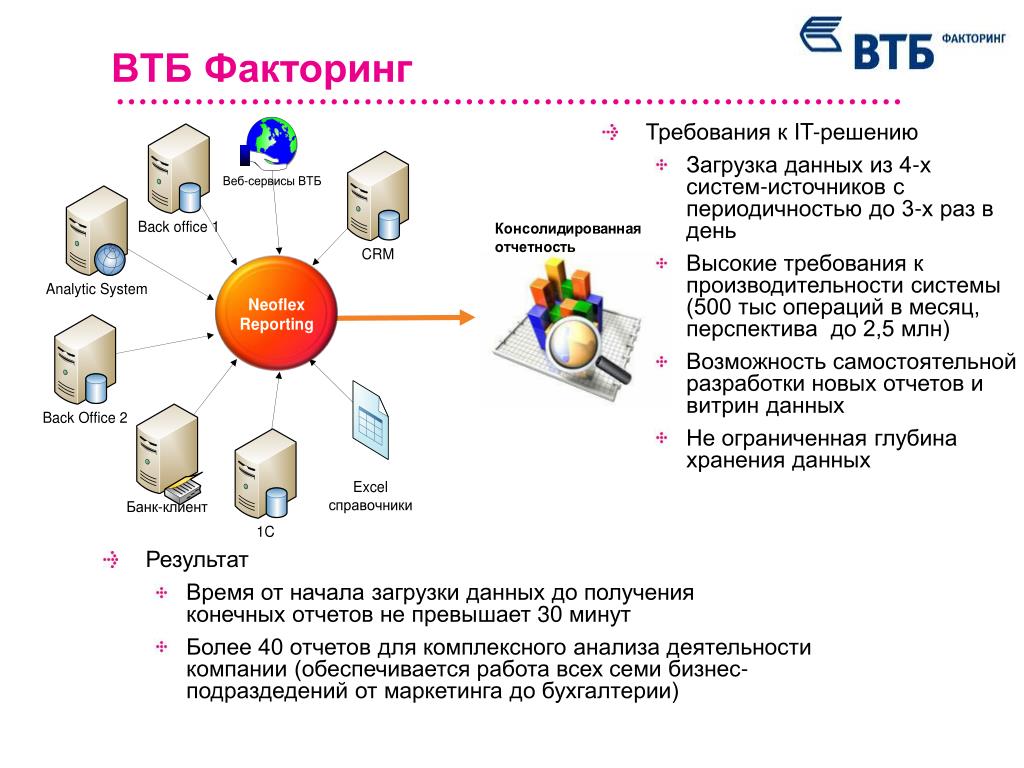 В факторизованной форме многочлен записывается как 5 x (3 x 2 + x — 5).
В факторизованной форме многочлен записывается как 5 x (3 x 2 + x — 5).